TreeRPO: Hierarchical Credit Assignment for Reasoning in Language Models
1. Introduction
Large language models (LLMs) have achieved impressive capabilities across a wide range of tasks, from natural language understanding to code synthesis and mathematical reasoning. However, for tasks that involve structured, multi-step reasoning such as solving math problems or generating proofs current fine-tuning techniques often struggle to produce robust and reliable outputs. A central challenge in these domains lies in the fact that correctness is typically assessed only after the entire output is generated, making it difficult to assign credit to specific reasoning steps. We refer to this evaluation regime as deterministic correctness.
1.1 Reinforcement Learning from Human Feedback: The PPO Framework
Reinforcement Learning from Human Feedback (RLHF) has become a foundational approach for aligning pretrained language models with desired behaviors or task objectives . Among RLHF techniques, Proximal Policy Optimization (PPO) stands out as the standard method, adopted widely due to its stability and efficiency.
Proximal Policy Optimization (PPO) is a widely used reinforcement learning algorithm, especially for fine-tuning large models with human or programmatic feedback (Schulman et al., 2017). PPO follows an actor-critic design: a policy network (the “actor”) proposes actions, and a value network (the “critic”) estimates how good those actions are. During training, the critic provides a baseline estimate of expected reward so the actor knows if its chosen action did better or worse than expected.
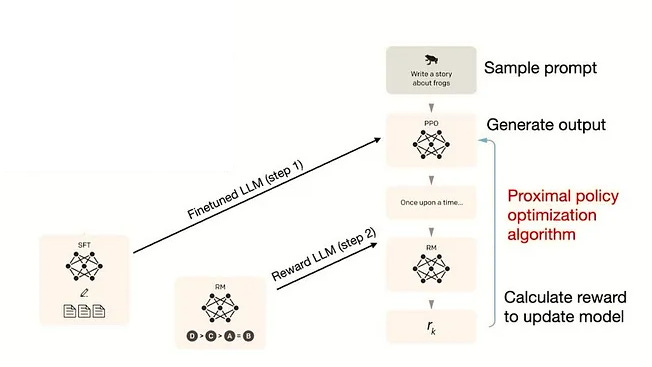
In practice, PPO’s actor-critic setup requires maintaining two models (policy and value), effectively doubling memory and compute requirements. Despite this, PPO became a standard algorithm in RLHF pipelines, as it balances performance and stability well. For instance, InstructGPT used PPO to fine-tune large language models with human preference signals (Ouyang et al., 2022).
1.2 Moving Beyond PPO: Group Relative Policy Optimization (GRPO)
Group Relative Policy Optimization (GRPO) was introduced by the DeepSeek team as a streamlined alternative to PPO (Liu et al., 2024a). GRPO removes the separate critic network entirely and instead derives the baseline from peer comparison. For each prompt, the policy samples a group of candidate responses and scores them with an external reward function. Each response’s advantage is defined relative to the group’s average score: outputs that perform better than their peers receive positive credit, while below-average ones are suppressed.
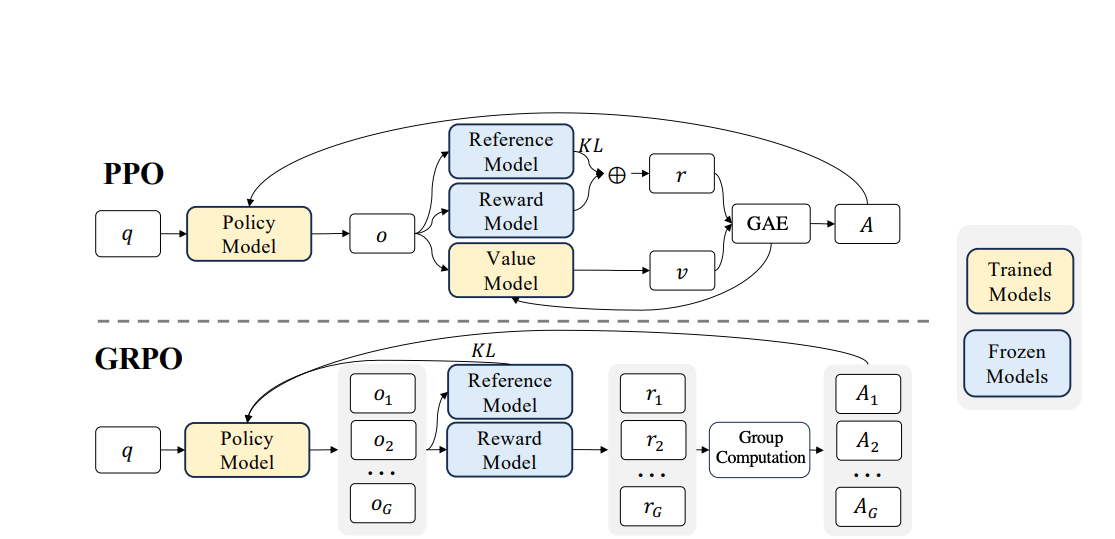
This group-relative baseline offers two practical benefits:
Lower computational cost – only a single policy model is trained (no actor–critic pair).
Built-in ranking signal – feedback depends on how well a response fares compared to others regardless of how the reward itself is computed. The reward can come from a learned preference model (as in DeepSeek’s general alignment experiments) or from a deterministic rule-based checker for example, DeepSeekMath grants a binary reward via an exact-match verifier of the boxed answer, with no reward model at all (Liu et al., 2024b,).
However, GRPO still inherits a critical weakness on tasks with deterministic correctness: the reward signal is broadcast uniformly to every token in the sequence. Because the final answer is judged in an all-or-nothing fashion, every token whether it contributed to sound reasoning or introduced the fatal error receives exactly the same advantage update. Valid intermediate steps are penalized together with the mistake that breaks the solution, and early missteps are rewarded if the final guess happens to be correct. This flat credit assignment ignores the hierarchical dependencies of multi-step reasoning and gives the model no guidance on where in the trajectory it should improve.
2. Introducing TreeRPO: Structuring Reasoning as a Tree
2.1 High-level Motivation and Intuition
While GRPO simplifies reinforcement learning by comparing candidate completions within a group, it assigns the same reward uniformly to every token in the generated sequence. This uniform reward becomes problematic in tasks judged by deterministic correctness such as math problem-solving or code generation with unit tests where correctness typically depends on the entire generated output. For instance, a correct reasoning process could be disrupted by a minor arithmetic mistake or syntax error at the end, causing the entire solution to fail. Under GRPO’s uniform credit assignment, tokens responsible for correct intermediate reasoning are penalized equally with those causing mistakes, making it difficult for the model to identify exactly where improvements are needed.
To address the fundamental limitations inherent in GRPO for deterministic correctness scenarios, we introduce TreeRPO, a hierarchical extension of GRPO that explicitly structures reasoning processes as branching trees. Inspired by the Tree of Thought (ToT) paradigm (Yao et al., 2023), which models reasoning as a branching process at inference time, TreeRPO integrates this idea directly into the training phase of reinforcement learning.
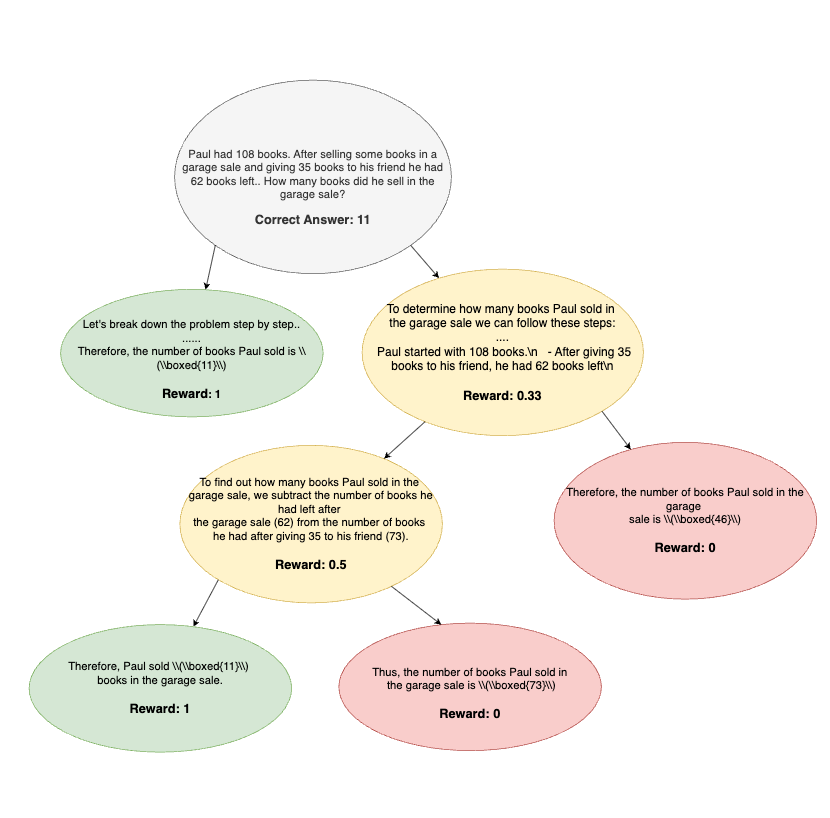
In TreeRPO, each node in the reasoning tree corresponds intuitively to a single "thought" or partial solution step, allowing the model to explicitly explore alternative reasoning paths. To determine the reward for these intermediate nodes, we look at all final solutions (leaves) branching out from them, and assign each node a reward based on the fraction of correct final answers among its descendants. In other words, each intermediate node receives feedback that directly reflects how effectively it contributes to producing correct solutions downstream, enabling the model to clearly identify and reinforce promising reasoning steps. By explicitly decomposing reasoning into structured segments during training, TreeRPO naturally addresses GRPO’s core limitation, providing precise and meaningful feedback at every step of the reasoning process.
2.2 From Intuition to Training: How TreeRPO Builds its Reasoning Tree
TreeRPO converts the “reward each thought” idea into three concrete steps.
1. Branching.
When a partial thought reaches a natural boundary and appears both substantive and uncertain, we fork into a small number of alternative continuations (typically two; see §3.2.1 for the precise gating criteria)
2. Prompt construction.
For every new node, TreeRPO simply concatenates all text produced along the path from the root, so each continuation sees the full history of prior “thoughts.”
3. Reward propagation.
Each leaf is graded with a binary correctness check. An interior node’s reward is the average of its descendant leaves, turning sparse pass/fail signals into smooth [0,1] feedback at every level. Sibling-relative advantages follow GRPO’s rule;
With one tree grown per training prompt, this procedure supplies rich, step-level learning signals while requiring no additional external evaluations beyond the usual final-answer checker.
2.3 TreeRPO vs GRPO - Key Advantages
2.3.1 Hierarchical Credit Assignment
GRPO propagates one scalar advantage uniformly to every token in a completion. A single mis-typed digit therefore penalises all earlier, correct deductions, while a lucky final guess rewards the entire sequence. TreeRPO breaks the sequence into discrete thought nodes and evaluates each node through the accuracy of its descendant leaves. Correct reasoning segments are reinforced, and the precise node that introduced the fatal error is down-weighted. In effect, the policy receives an itemised bill of which steps helped and which harmed, rather than a single, undifferentiated total.
2.3.2 Outcome–Process Hybrid Supervision
Two reward philosophies dominate the literature: Outcome Reward Modelling (ORM), which scores only the final answer, and Process Reward Modelling (PRM), which attempts to grade intermediate reasoning with domain-specific heuristics. ORM is objective but sparse; PRM is informative but subjective. TreeRPO fuses the strengths of both. It retains ORM’s binary pass/fail decision at the leaves, yet structurally distributes that verdict upward so every interior node inherits a reward that reflects the quality of the sub-trajectory beneath it. The model thus benefits from process-level guidance without inventing new heuristics it is still learning solely from the task’s ground-truth checker.
2.3.3 Smooth Rewards & Targeted Exploration
Averaging binary leaf rewards converts an all-or-nothing signal into continuous values r(n) ∈ [0,1] for every interior node. Even when most final answers in a tree are wrong, partial branches that made progress still yield higher intermediate rewards, preserving a learning gradient. Complementing this, TreeRPO initiates new branches only when the model’s entropy exceeds a threshold H_th. Exploration is therefore concentrated where the policy is uncertain, rather than sampling whole extra completions indiscriminately as GRPO does. The combination of smooth feedback and uncertainty-driven branching accelerates learning while keeping compute overhead modest.
![Figure 1. Flat versus hierarchical credit assignment. Top (GRPO): Two full completions share the same prefix but diverge at the end; one is wrong [ 𝑟 = 0 ] [r=0] and one correct [ 𝑟 = 1 ] [r=1]. GRPO broadcasts each scalar reward uniformly across every token in its completion. Bottom (TreeRPO): The shared prefix forms a single root node that branches into the same two endings. The correct and incorrect leaves receive rewards 1 1 and 0 0, respectively, so the shared prefix inherits their average [ 𝑟 = 0.5 ] [r=0.5]. TreeRPO thus pinpoints credit (or blame) to the exact segment where the reasoning paths diverge, instead of treating the entire sequence as equally responsible.](https://substackcdn.com/image/fetch/$s_!yinB!,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2F45de759b-fdce-43cd-a270-da0bf8316300_1073x396.png "Figure 1. Flat versus hierarchical credit assignment. Top (GRPO): Two full completions share the same prefix but diverge at the end; one is wrong [ 𝑟 = 0 ] [r=0] and one correct [ 𝑟 = 1 ] [r=1]. GRPO broadcasts each scalar reward uniformly across every token in its completion. Bottom (TreeRPO): The shared prefix forms a single root node that branches into the same two endings. The correct and incorrect leaves receive rewards 1 1 and 0 0, respectively, so the shared prefix inherits their average [ 𝑟 = 0.5 ] [r=0.5]. TreeRPO thus pinpoints credit (or blame) to the exact segment where the reasoning paths diverge, instead of treating the entire sequence as equally responsible.")
3. Mathematical Details & Algorithm
3.1 Mathematical Details
3.1.1 Notation and Tree Structure
Policy.
π_θdenotes the current policy model. We do not maintain a reference policy, so we set the KL regularization coefficient β to 0, following recent Dr-GRPO (Chen et al., 2025) that have demonstrated stable optimization without explicit KL terms.Node. Each node
nproduces a text spano_n(treated as one action) given the concatenated contextc_nof all its ancestors.Children and leaves.
C(n)is the set of direct children ofn;L(n)is the set of all leaf nodes that descend fromn.
3.1.2 Reward Propagation
A deterministic checker assigns every leaf node l in L(n) a binary reward:
The reward of any interior node n is the mean correctness of its descendant leaves:
3.1.3 Sibling-Relative Advantage and Loss
Following the “direct-relative” formulation of GRPO (Liu et al., 2024a) and the no-standard-deviation variant advocated in Dr-GRPO (Chen et al., 2025), each node’s advantage is
where sib(n) is the set of siblings of n (including n itself).
Define the likelihood ratio
We minimise the GRPO-style surrogate objective-
3.2 Training Workflow
Each training iteration proceeds through four plain-language stages.
3.2.1 Generate a reasoning tree
Starting from the root prompt, the policy π_θ unfolds a tree of candidate thoughts to a maximum depth of k = 7. A split (i.e., sampling two new child continuations from the current node) occurs only when all of the following hold:
the node ends at a natural delimiter - period (
.), newline, or similar punctuation;the node length exceeds a tunable minimum
L_min;the model’s next-token entropy is above threshold
H_th; The entropy is evaluated immediately after producing the delimiter, so it reflects the model’s uncertainty about what should come next if the segment were to continue.the current depth is still below
k.
There are two practical exceptions:
Forced first split. Before the very first token, TreeRPO forces a branch, creating exactly two depth-1 children.
Coverage split on an overly long leaf. When generation stops, if the final leaf is longer than a separate length cap
S_min, the algorithm “rewinds” to the leaf’s parent and samples an extra sibling branch. Consequently the last branching point may have up to four children, ensuring that most of the generated text is covered by reward sampling.
3.2.2 Diversified branch tokens
When a regular split is triggered (that is, the four branching conditions are met), TreeRPO always forces the new child continuation to begin with a different next token from the one already selected in the current path.
In other words, the token used to start the alternative branch must satisfychosen_token ≠ already_selected_token
as measured in the entropy calculation.
This guarantees the two branches explore distinct trajectories rather than duplicating the same high-probability continuation.
3.2.3 Score the leaves.
Every leaf completion is passed to a deterministic checker that returns 1 for fully correct and 0 for incorrect.
3.2.4 Propagate rewards.
Rewards flow bottom-up: a node’s reward is the average correctness of all leaves beneath it. This converts sparse pass/fail signals into smooth values in [0, 1] at every non-leaf node.
3.2.5 Update the policy.
Using the sibling-relative advantages defined in Section 3.1 and the GRPO-style loss, TreeRPO applies one gradient step over all nodes in the tree effectively delivering token-level guidance without a critic network.
TreeRPO Training Loop
Inputs:
• Dataset D # list or stream of training prompts
• Policy parameters θ # current model πθ
• Max depth k ← 7
• Length thresholds L_min, X (X > L_min)
• Entropy threshold H_th
• Clipping parameter ε ← 0.2 # PPO / GRPO style
Initialize:
repeat
▸ Snapshot current policy π_old ← πθ
for each prompt q in D do
# ---- 1. Build a reasoning tree --------------------------
T ← {root node n0 with context q}
expand_two_children(n0, force_distinct_tokens=True) # forced first split
while nodes_to_expand(T) do
choose next leaf node n
if depth(n) < k
and ends_with_delimiter(n)
and len(n) ≥ L_min
and entropy(n) > H_th
then
expand_two_children(n, force_distinct_tokens=True)
# Coverage split for overly long final leaves
for each leaf l in T :
if len(l) > X then
parent ← parent(l)
expand_extra_sibling(parent, force_distinct_tokens=False)
# ---- 2. Evaluate leaves & propagate rewards -------------
for each leaf l in T :
r(l) ← deterministic_checker(l) # 0 or 1
propagate_means_upwards(T) # Eq. (2)
# ---- 3. Compute advantages & accumulate loss -------------
for each node n in T :
A(n) ← r(n) − mean_{s in sib(n)} r(s) # Eq. (3)
ρ ← πθ(o_n | c_n) / π_old(o_n | c_n)
L ← − min( ρ · A(n),
clip(ρ, 1−ε, 1+ε) · A(n) ) # Eq. (5)
accumulate_gradient(L)
# ---- 4. Policy update ---------------------------------------
θ ← optimizer_step(θ, accumulated_gradient)
4. Experimental Setup
To provide a direct comparison with a well-established GRPO system, we follow the general training stages used for Qwen 2.5-Math-1.5B-Instruct. In Qwen’s approach, large-scale supervised fine-tuning is performed on approximately 2.5 million Chain-of-Thought (CoT) examples, followed by GRPO training on 66,000 prompts with reward model supervision. For our experiments, we use the same base model Qwen/Qwen2.5-Math-1.5B - but train with only 5,000 examples for each phase. We omit the reward model entirely and replace GRPO with TreeRPO, using deterministic correctness as the reward signal.
4.1 Data and Splits
All supervision comes from the NuminaMath-CoT dataset (≈860K problems).
We sample two non-overlapping 5K subsets: one for the SFT phase, containing full chain-of-thought (CoT) solutions, and another for TreeRPO, where only the final boxed answers are used to compute correctness.
4.2 Training Regime
4.2.1 Supervised Fine-Tuning
We fine-tune the base model on a set of 5,000 supervised examples for one epoch. The resulting checkpoint is then used as the starting point for TreeRPO training.
4.2.2 TreeRPO Training
We train TreeRPO for one epoch over its 5K prompts on a single RTX 4090 GPU (48 GB), which completes in roughly 18 hours. The setup uses a lightweight GRPO-style objective.
Key hyperparameters:
Split criteria:
Segment length ≥ L_min = 150
Next-token entropy (top-20 logits) ≥ H_th = 1.0
k = 7(max tree depth)
Sampling for child completions:
Temperature = 0.6
Top-p = 0.85
Top-k = 25
Repetition penalty = 1.1
5. Results & Analysis
5.1 Training Analysis
To better understand TreeRPO’s training behavior, we first examine how key metrics such as average reward, training loss, exploration depth, and tree structure evolve throughout the training process. This analysis highlights how TreeRPO gradually learns from its structured feedback and adjusts its exploration strategy accordingly.
Panel (a) shows that the average leaf-level reward rises from about 0.48 at the start of training to a plateau in the 0.64–0.66 range, displaying the familiar RL trend of quick early improvement that gradually levels off with some noise. Meanwhile, panel (c) shows that after an initial phase of wide exploration, the average tree size stabilizes by around 3,000 questions at 66 ± 3 leaves per problem a token budget lower than sampling 66 full completions in GRPO. Overall, TreeRPO appears to prune unproductive branches more efficiently over time, reducing token usage while incrementally increasing the proportion of correct answers.
Panel (f) indicates that correct solutions often correspond to shorter answer lengths, while incorrect leaves especially at greater depths tend to be much longer and more variable, raising the possibility that unproductive branches sometimes spiral into unnecessarily lengthy reasoning. Panel (d) shows that larger trees are generally associated with higher error rates, hinting that TreeRPO does tend to allocate more exploration to harder problems. However, the wide error bars and considerable overlap also suggest that this process is far from perfect, and the relationship between exploration depth and success is not absolute
5.2 Results
We evaluate TreeRPO on the official GSM8K test set (1,319 problems) to assess its math reasoning accuracy compared to Qwen2.5-Math-1.5B-Instruct. Accuracy is measured under two decoding strategies: (1) Greedy decoding, which uses temperature 0 (no sampling) to reflect single-pass reliability; and (2) Maj@8 self-consistency, in which eight completions are sampled (temperature 0.7, top-p 0.8, matching Qwen’s reported settings) and a majority vote is taken over the extracted final \boxed{…} answers. Table 1 summarizes the results.
6 Conclusion and Future Directions
In summary, TreeRPO demonstrates a number of practical benefits compared to existing approaches. Whereas Qwen’s recipe relies on approximately 2.5 million supervised Chain-of-Thought (CoT) examples and a further 66,000 prompts with reward-model supervision, our TreeRPO setup achieves competitive accuracy with just 5,000 SFT examples and 5,000 RL fine-tuning problems requiring two orders of magnitude less labeled data. Additionally, TreeRPO eliminates the need for a reward model entirely, learning directly from a deterministic checker and its own hierarchical structure, in contrast to the extra infrastructure required by GRPO. Despite this much lighter training setup, TreeRPO slightly outperforms the Qwen Math Instruct baseline on GSM8K, achieving 86.4% accuracy with greedy decoding and 89.6% with Maj@8, compared to Qwen’s 84.8% and 89.5%, respectively. These results suggest that hierarchical credit assignment can deliver equal or better performance with significantly less labeled data and simpler training infrastructure.
At the same time, there is still plenty of room to refine the method. The explore-exploit question of when to branch and how many branches to spin off currently relies on simple, hand-tuned rules. A natural next step would be to replace those rules with a lightweight “splitter” network that is trained alongside the policy and learns, in real time, both whether the model should branch and how aggressively it should do so. Beyond smarter branching, since this method naturally yields more precise, per-token reward signals, it opens the door to replacing standard reward models with ones that assign feedback at the token or clause level allowing us to use these finer-grained signals to provide more targeted feedback during training. Finally, since TreeRPO relies only on a deterministic checker, this approach could potentially be used for other pass/fail domains, such as code synthesis with unit tests, and may offer a broadly useful tool for structured reasoning tasks.
Link to model: Hugging Face TreeRPO Model
REFERENCES
Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal Policy Optimization Algorithms. arXiv preprint arXiv:1707.06347.
Liu, X., Wang, Y., & Li, Z. (2024). Group Relative Policy Optimization. arXiv preprint arXiv:2402.03300.
Chen, Q., et al. (2025). Dr‑GRPO: No‑Variance Normalized Group Relative Policy Optimization. arXiv preprint arXiv:2503.20783.
Yao, S., et al. (2023). Tree of Thoughts: Deliberate Problem Solving with Large Language Models. ArXiv.
Ouyang, L., et al. (2022). Training language models to follow instructions with human feedback. Advances in Neural Information Processing Systems.
Yang, A., Zhang, B., Hui, B., et al. (2024). Qwen 2.5-Math Technical Report: Toward a Mathematical Expert Model via Self-Improvement. arXiv:2409.12122